滷蟲屬
[拼音]:LiMan jihexue
[英文]:Riemannian geometry
德國數學家(g.f.)b.黎曼在19世紀中期所提出的幾何學理論。1854年,他在格丁根大學發表的就職演說,題目是《論作為幾何學基礎的假設》,可以說是黎曼幾何學的發凡。從數學上講,他發展了空間的概念,首先認識到幾何學中所研究的物件是一種“多重廣延量”,其中的點可以用n個實數作為座標來描述,即現代的微分流形的原始形式,為用抽象空間描述自然現象打下了基礎。更進一步,他認為,通常所說的幾何學只是在當時已知測量範圍之內的幾何學,如果超出了這個範圍,或者是到更細層次的範圍裡面,空間是否還是歐幾里得的則是一個需要驗證的問題,需要靠物理學發展的結果來決定。他認為這種空間(也就是流形)上的幾何學應該是基於無限鄰近點之間的距離。在無限小的意義下,這種距離仍然滿足勾股定理。這樣,他就提出了黎曼度量的概念。這個思想發源於c.f.高斯。但是黎曼提出了更一般化的觀點。在歐幾里得幾何中, 鄰近點的距離平方是

(在笛卡兒座標下),這確定了歐幾里得幾何。但是在一般曲線座標下,則應為

,這裡

是相當特殊的一組函式。如果

是一般的函式,又(gij)仍構成正定對稱陣,那麼從

出發,也可以定義一種幾何學,這便是黎曼幾何學。由於在每一點的周圍,都可以選取座標使得在這點成立
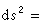

,所以在非常小的區域裡面勾股定理近似成立。但在大一點的範圍裡一般就和歐幾里得幾何學有很大的區別了。
黎曼認識到距離只是加到流形上的一個結構,因此在同一流形上可以有眾多的黎曼度量,從而擺脫了經典微分幾何曲面論中侷限於誘導度量的束縛。這是一個傑出的貢獻。
其後,E.B.克里斯托費爾、g.裡奇等人又進一步發展了黎曼幾何,特別是裡奇發展了張量分析的方法,這在廣義相對論中起了基本的作用。1915年A.愛因斯坦創立了廣義相對論,使黎曼幾何在物理中發揮了重大的作用,對黎曼幾何的發展產生了巨大的影響。廣義相對論真正地用到了黎曼幾何學,但其度量形式不是正定的,現稱為洛倫茨流形的幾何學(見廣義相對論)。
廣義相對論產生以來,黎曼幾何獲得了蓬勃的發展,特別是É.嘉當在20世紀20~30年代開創並發展了外微分形式與活動標架法,建立起李群與黎曼幾何之間的聯絡,從而為黎曼幾何的發展奠定了重要基礎且開闢了廣闊的園地,影響極為深遠,由此還發展了線性聯絡及纖維叢方面的研究。半個多世紀以來,黎曼幾何的研究也已從局部發展到整體,產生了許多深刻的並在其他數學分支和現代物理學中有重要作用的結果。隨著60年代大範圍分析的發展,黎曼幾何和偏微分方程(特別是微分運算元的理論)、多複變函式論、代數拓撲學等學科互相滲透、互相影響。在現代物理中的規範場理論(又稱楊-米爾斯理論)中,黎曼幾何也成了一個有力的工具。
黎曼流形
黎曼幾何是黎曼流形上的幾何學。黎曼流形指的是一個n維微分流形M,在其上給定了一個黎曼度量g,也就是說,在微分流形M的每一個座標鄰域(U,x)內,用一個正定對稱的二次微分形式


來度量二個無限鄰近的點(x1,x2,…,xn)和(x1+dx1,x2+dx2,…,xn+dxn)之間的距離。這裡(gij)構成一個正定對稱的n×n陣,並假設gij(x)關於(xi)有一定的可微性,而M上連線兩點
P
、Q
的曲線C
:xi=xi(t),α≤t≤b的長度l(C
)就用積分
來計算。為了保證距離的度量與座標鄰域的選取無關,還要求gij滿足二階協變張量的變換規律,用整體黎曼幾何的語言來說,就是在微分流形M上給定了一個由分量gij決定的正定對稱二階協變張量場g。M連同g,即(M,g)稱為一個n維黎曼流形,g稱為度量張量或基本張量。由於歷史的原因,黎曼流形又常稱黎曼空間,但後者偏重於區域性意義,即常指黎曼流形的一個開子集或一個座標鄰域。
度量張量g在流形M每點
P
(x1,x2,…,xn)的切空間Tp(M)中就規定了一個內積gp(或記為:〈,〉)用來計算切向量的長度、交角。即若向量X,Y∈Tp(M),而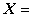
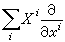
,

,則X 的長度
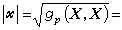

;X、Y的交角 θ由


,0≤θ≤π決定。如果cosθ=0,即

,就稱X、Y 為互相正交。│尣│=1的向量稱為單位向量,Tp(M)中由兩兩互相正交的單位向量組成的基稱為正規正交基,對任一點
P
∈M,在P
點的某一鄰域U 內總存在n個單位向量場e1,e2,…,en,使得在U的每點它們構成切空間的一個正規正交基,這n個區域性向量場稱為一個區域性正規正交基或區域性正規正交標架。運用區域性正規正交標架來研究黎曼幾何的方法稱為活動標架法。黎曼幾何中的許多公式和幾何量在活動標架下有特別簡單明瞭的表示式,例如取ω1,ω2,…,ωn為區域性正規正交標架e1,e2,…,en的對偶形式,也稱對偶基,即滿足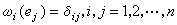
的n個一次微分形式,於是在基{ei}下,由於

,度量形式可寫為

。
任一仿緊微分流形總具有黎曼度量,這種黎曼度量的數目是非常繁多的,但也不是完全任意的。微分流形的度量結構是受它的拓撲結構所制約的,而這種制約關係正是黎曼幾何研究的一個重要內容,還存在許多沒有解決的問題。
有了計算曲線長度的方法,黎曼流形(M,g)上任意兩點
P
、Q
之間的距離d(P
,Q
)就可以用M中連線P
、Q
的所有分段可微分曲線的長度的下確界來定義,即d(P, Q)=inf(l(
C
)),(連線
P
,Q
的分段可微分曲線C
)。於是,M在上述距離下成為一個度量空間,還可以證明,它所匯出的度量拓撲與流形M原有的拓撲是等價的。聯絡、平行移動
歐氏空間中兩不同點的切向量可以用平行移動的方法移動到同一點處加以比較,而且這種平行移動與移動的道路無關。黎曼流形上不同點的切向量也可以用平行移動的方法加以比較,但一般說來,這時由於流形的彎曲,平行移動與移動的道路有關。設
P
(xi)為流形上任一點,{ei},i=1, 2,…,n為P
點附近的一個區域性標架,P
+dP
為P
的一個無限鄰近點,座標為xi+dxi。定義P
+dP
點的切空間和P
點的切空間的一個線性對應,使得P
+dP
點的
對應於
P
點的向量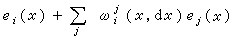
,這裡

是n2個一次微分形式, 稱為聯絡形式, 這樣引入的對應稱為無窮小平行移動。設

是
P
點附近的一個區域性向量場,那麼在點P
+dP
的向量
·
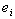
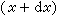
經過無窮小平行移動至
P
點後就會得到向量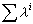


, 它與
P
點的向量
在一階無窮小範圍內的差
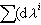



稱為向量場

的協變微分又稱絕對微分,記為DX,


,特別有標架基ei的協變微分為
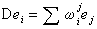
。
為了可以在流形上整體地定義平行移動,自然要求這樣定義的無窮小平行移動與標架的選取無關,即應該保證在標架改變時這樣所確定的平行移動和協變微分不受影響。令

表示標架的變換,則

(i,j=1,2,…,n)(1)
就是在標架變換下聯絡形式的變換規律,這裡(
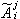
)是(
A

)的逆陣。
如果在黎曼流形(M,g) 的各點關於每個標架給定了n2個一次微分形式 {ω

},它們之間滿足變換規律(1),就稱在M上給定了一個仿射聯絡或稱線性聯絡(見聯絡論),{ω

}為相應的聯絡形式。
設{ωi}為標架{ei}的對偶基,則
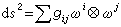
,這裡

。容易看出在標架變換

下,應有

。由此,在標架變換下還成立下述兩個關係:
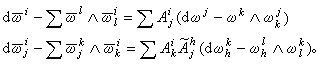
因此,如記

,(2)

,(3)
那麼

都分別是一個張量的分量。這就是說,在標架的變換下,應成立
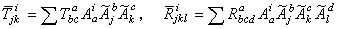
相應的張量分別稱為仿射聯絡的撓率張量和曲率張量。撓率張量等於零的仿射聯絡則稱為無撓率的聯絡。
黎曼聯絡、列維-齊維塔平行移動
黎曼聯絡是黎曼流形上最重要和最常用的一種聯絡。構造如下:設{ei}為關於座標系(xi)的自然標架,即

,此時

。令
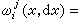

式中

稱為第二類克里斯托費爾符號,(gij)為(gij)的逆陣,則不難驗證{ω
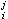
}決定了一個仿射聯絡而且滿足下列二個性質:
(1)是無撓率的;
(2)相應的無窮小平行移動保持向量的內積。滿足①和②的仿射聯絡稱為黎曼聯絡,也稱列維-齊維塔聯絡,這種聯絡是惟一的,在自然標架下它就是如上決定起來的。黎曼流形上如果無特殊說明都是用黎曼聯絡。
在自然標架下,向量場

的協變微分DX可以表達為

,即分量為

的張量。如果

為另一個向量場,稱向量

為X關於Y的協變導數,記為墷

X。容易看出成立下面的性質:
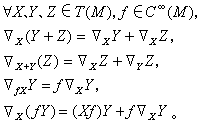
應用這個符號,黎曼聯絡的兩個性質可表達為:
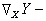


,這裡[X,Y]=XY-YX是向量X,Y 的換位運算。特別在正規正交標架下,由

可以推得聯絡形式ω

關於指標i,j反稱,即

。
設T 表示黎曼流形(M,g)上一條曲線с的切向量,X是с上的向量場,如果墷TX=0,即X關於с的切向量的協變導數為零,就稱X沿著曲線с平行或稱X是曲線с上的平行向量場。在區域性座標系(x)下,若

,那麼, X 沿 с平行的條件為 λi(x) 滿足常微分方程組∶

,反之,在任意點
P
(x)給定初始向量
,解上述常微分方程組就可得到с上的一個平行向量場,稱為向量X0沿с平行移動生成的向量場,這種關於黎曼聯絡的平行移動也稱為列維-齊維塔平行移動。
和樂群
從上面所述不難看出一個向量沿著不同的曲線平行移動到同一點所得到的向量一般是不同的,這種差異刻畫了黎曼流形的彎曲程度。設
P
是(M,g)的任一點,l(P
)表示以P
為始點和終點的閉曲線的集合,如果с1、с2是l(P
)中的元素,則複合曲線с1·с2也是l(P
)中的元素。對X ∈Tp(M)沿著l(P
)中元素C
平行移動回到P
點就得到 X┡∈Tp(M),這樣l(P
)中的一個元素就對應於 Tp(M)→Tp(M)的一個同構。這種同構全體構成的群就稱為在P
點處的和樂群,當M是連通流形時,不同點的和樂群是同構的,和樂群在黎曼幾何的研究中有重要的作用。張量的協變微分
由向量的協變微分還可引出張量場的協變微分。在任意的標架{ei}下,設對偶基為{ωi},聯絡形式為{ω

},α階反變b階協變的張量場T 在(x)點的分量記為
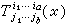
,則T 的協變微分就是


是一個α階反變b+1階協變的張量的分量,稱為

的協變導數。特別,若

是T 在自然標架下的分量,那麼,
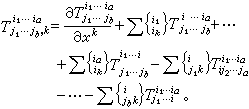
結構方程、比安基恆等式
關於黎曼聯絡方程 (2)和(3)成為:

(4)
方程(4)稱為黎曼流形的結構方程。
在自然標架下,從結構方程可以算得曲率張量的分量

用基本張量gij將指標h拉下得到分量為

的一個四階協變張量,也稱為曲率張量,它反映出一個向量沿無限小環路平行移動回到原處所受到的變差,體現出空間的彎曲。不難驗證下述關係式:
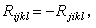

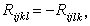

進一步外微分結構方程中的第二式並利用第一式可得下面的第二比安基恆等式:

。
曲率張量是黎曼幾何中最重要的張量之一。在 n=2的場合,可以看出惟一的獨立分量是R1212。而當M是三維歐氏空間E3中曲面時, 關於誘導度量在正規正交基下的R1212恰好是曲面的高斯曲率K。高斯-博內公式揭示了曲率張量與流形的尤拉示性數的內在聯絡,用纖維叢的思想證明了它的高維推廣是陳省身的傑出成果之一。
截面曲率、裡奇曲率、數量曲率
在任一點
P
處的二個獨立切向量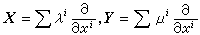
決定了
P
點的一個二維切平面πp(X,Y),稱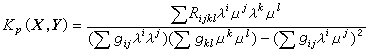
為πp(X,Y)的截面曲率也稱黎曼曲率。可以驗證同一二維切平面的截面曲率與基向量X,Y 的選取無關。
截面曲率完全決定了曲率張量,也就是說,如果在一點
P
知道了所有的截面曲率, 那麼在這點的曲率張量就決定了。另外,截面曲率滿足下面的舒爾定理:如果在連通的黎曼流形(M,g)(n≥3)的各點,截面曲率與方向X,Y無關,那麼它與點也無關,因而是常數。這種黎曼流形稱為常曲率黎曼空間。常曲率為K 的黎曼流形的曲率張量滿足條件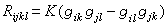
。
由曲率張量縮並而得的張量,即分量為
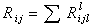
的二階協變對稱張量稱為裡奇張量 。 設

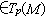
,由

決定的量稱為在
P
點X方向的裡奇曲率。由
決定的數量函式S 稱為在
P
點的數量曲率。截面曲率、裡奇曲率以及數量曲率是非常重要的幾何量。研究這些量與黎曼流形的幾何性質以及拓撲性質之間的關係是黎曼幾何的一個重要課題。例如,嘉當-阿達馬定理斷言:若一個n維單連通完備黎曼流形的截面曲率處處不大於零,那麼它與Rn微分同胚。再如邁爾斯定理斷言:若完備黎曼流形的裡奇曲率處處大於一個正常數h,那麼它必是緊流形而且基本群有限。W.克林格貝格和M.伯熱證明的球定理斷言:如果完備單連通n維黎曼流形M的截面曲率KM 滿足

,那麼M與n維歐氏球面Sn同胚。這些結果顯示了流形的拓撲性質與度量性質之間有密切的聯絡。在這方面還有許多未解決的問題。
測地線、完備黎曼流形
n 維歐氏空間En中連線兩點
P
、Q
的直線段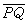
是連線
P
、Q
的所有曲線中最短的,而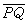
的長度就等於
P
、Q
的距離。 假設C
2曲線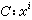
=
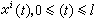
是連線
P
、Q
的最短線,t是C
的弧長引數,即
。考慮
C
的任意一族變分曲線
0≤t≤

,-ε≤s≤ε,即對固定的s,曲線
C
s是連線P
、Q
的曲線,且C
0=C
。顯然C
滿足
0,也即最短線必是長度泛函的臨界點,由尤拉-拉格朗日方程得到
C
應滿足下列微分方程組:
。(5)
稱滿足方程(5)的曲線為測地線,歐氏空間中的測地線就是直線,歐氏球面中的測地線是大圓弧。最短線必是測地線,但反之則不一定成立。例如,歐氏球面上以
P
、Q
為端點的大圓優弧雖是測地線卻不是連線P
、Q
的最短線(應為劣弧)。然而,在區域性範圍內測地線總是最短線,也就是說,任意點P
總存在一個區域性鄰域U,使得對U 中任意點Q
,惟一存在一條完全落在U內的測地線C
連結P
、Q
,而且C
的長度等於P
、Q
的距離。一條連線兩點P
、Q
的測地線,如果它的長度恰好等於P
、Q
的距離,就稱為極小測地線。顯然它就是連線P
、Q
的最短線。從(5)不難看出測地線的另一說法是:測地線是切向量沿自身平行的曲線,即墷TT=0。
方程組(5)是一個二階常微分方程組,因此任意給定一點
P
和P
點的一個單位切向量 X, 總惟一地存在一條測地線過P
點且在P
點與X相切。然而它未必能夠無限地延伸。而且任意兩點間就也不一定能用一條極小測地線連線。例如,設S2P
}為二維歐氏球面S2去掉一點P
而得到的曲面,於是處在過P
點的同一大圓上充分接近P
點而分居P
的兩側的兩點P
1、P
2之間就沒有極小測地線。如果一個黎曼流形(M,g) 的任意測地線都能被開拓成在整個t∈(-∞, +∞) 上定義的測地線,則(M,g)稱為完備黎曼流形,或稱度量張量 g是完備度量。例如,歐氏空間、歐氏球面等都是完備黎曼流形。任何緊黎曼流形(M,g)(即M本身是緊流形)都是完備黎曼流形。完備黎曼流形上任意兩點總能用一條極小測地線連線。這就是著名的霍普夫-裡諾定理所斷言的事實。
指數對映
設
P
為黎曼流形(M,g)上任意點,V為P
點切空間Tp(M)中一個向量,用γV(t)表示從P
點出發以V為初始切向量的測地線,即уV(0)=P
,γ塎
(0)=V,若γV(1)有定義,則對映expp∶V

γV(1)稱為
P
點的指數對映,可以證明:存在Tp(M)中原點的一個開鄰域U,使得expp是U到expp(U)的微分同胚,此時將expp(U)嶅M中點採用U 中原像點的座標為座標得到的座標稱為法座標, 相應的鄰域expp(U)稱為P
點的法座標鄰域。採用法座標系,許多幾何量有簡明的表示式,所以法座標系是黎曼幾何研究中常用的座標系。對於完備黎曼流形,指數對映expp在整個 Tp(M)上都有定義,但一般不是一對一的。黎曼子流形
用三維歐氏空間中的度量來計算曲面上的曲線長度就在曲面上誘導了一個度量,由此展開的微分幾何就是經典的曲面論。在黎曼幾何中,設M是m維黎曼流形(N,愡)的一個n維浸入子流形,i:M→N是包含對映。如果用N的黎曼度量愡 來計算M的曲線長度,那麼在M上得到一個誘導的黎曼度量g(記為i*愡 ),M關於誘導度量稱為N 的一個n維黎曼子流形,m-n稱為子流形的餘維數。如果(x1,x2,…,xn)和(y1,y2,…,ym)分別是 M和N 的區域性座標系,


,那麼
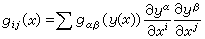

,m;i,j=1,2,…,n),N上在點
P
∈M的一個向量ξp,如果與M在P
點的每一切向量都正交,就稱為M在P
點的一個法向量。可以取N 的區域性正規正交標架{eα},使得限制在M上時,{ei}是M 的一個區域性正規正交標架,而{er},r=n+1,…,m,是M 的m-n個互相正交的單位法向量。設{ωα}是對偶基,{ω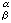
}是N 的黎曼聯絡形式,N 的結構方程為:

這裡
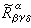
是N 的曲率張量,
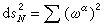
限制在M上時,

,即ωr=0,因此從第一個方程得到


。由嘉當引理

,且

,稱


為子流形M的第二基本形式,正像三維歐氏空間曲面論中一樣,第二基本形式在子流形的研究中起著十分重要的作用。N 的結構方程中的第二個方程限制於M上,並取指標α =i,β=j,與M的結構方程相比較,可以得到M的曲率張量

, 稱為子流形的高斯方程。如果再取其他的指標值,還可得到子流形的科達齊方程和裡奇方程。
由
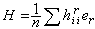
定義的法向量稱為黎曼子流形的平均曲率向量,如同曲面論一樣,平均曲率向量等於零的子流形稱為極小子流形。特別當子流形的維數等於 2時,稱為極小曲面。而餘維數等於 1時稱為極小超曲面。一維的極小子流形就是測地線。
極小子流形具有明顯的變分意義,它是體積泛函的臨界點。歷史上,極小子流形的研究與J.普拉託問題有密切的聯絡:設給定了空間中一條閉的可求長的若爾當曲線
C
,能否找到一個以C
為其邊界的極小曲面?極小子流形,特別是極小曲面的存在性,惟一性的分類問題構成了黎曼幾何研究的一個重要方面。當第二基本形式恆等於零,即

的極小子流形稱為全測地子流形。這時M中的任意一條測地線也是N中的測地線,或者說,M中的平行移動與在外圍空間N中的平行移動是完全一致的。
如果兩個黎曼流形(M,g)與(N,愡)之間存在對映ƒ∶M→N,使得ƒ(M)嶅N是N 的一個浸入子流形,且g正好是愡誘導而成的,就稱ƒ是(M,g)到(N,愡)的一個等距浸入。當ƒ(M)還是嵌入子流形時,就稱為等距嵌入。
一個黎曼流形(M,g)能否等距地浸入或嵌入到高維的歐氏空間中成為黎曼子流形以及這種浸入或嵌入的剛性問題是黎曼幾何中由來已久的重要而且有興趣的研究課題。
關於區域性等距嵌入,即黎曼流形的一個區域性區域等距嵌入到高維歐氏空間的問題,N.雅內特(1926)和É.嘉當(1927)證明了:每個p維的黎曼流形能區域性等距嵌入到En中,如果

。
關於整體等距嵌入問題,J.F.納什(1956)證明了:任何
P
維緊黎曼流形能整體等距嵌入到
維歐氏空間中,而非緊的黎曼流形能整體等距嵌入到

維歐氏空間中。
等距對映、共形對映、調和對映
黎曼幾何研究中另一個重要的課題是研究黎曼流形之間的一些有重要幾何意義和物理學背景的對映,其中包括等距對映、共形對映和調和對映等。
兩個黎曼流形(M,g)和(N,g┡)之間的一個對映ƒ,如果滿足

,其中 σ 是某一函式,即X,Y∈Tp(M)成立

,則稱ƒ為共形對映。特別當M與N 的維數相等而且ƒ是微分同胚時,則稱(M,g)共形同胚於(N,g┡),如果此時還有σ呏0,即ƒ*g┡=g,則稱ƒ是等距對映。
從定義可以看出,在共形對映下兩向量的夾角保持不變,而在等距對映下向量的長度也保持不變。如果一個n維黎曼流形(M,g)的任意點都有一個座標鄰域(U,x),使得在U內度量張量

,即g區域性共形於平坦度量δij,就稱為共形平坦黎曼流形。
任何一個二維黎曼流形都是共形平坦的,這是由於在等溫座標下,度量張量可表為eσ(dx2+dy2)的形式。
在n>3時,共形平坦黎曼流形的特徵是用下面定義的張量來刻畫的:設在區域性座標系下,黎曼流形(M,g)的度量張量、曲率張量、裡奇張量的分量分別為

,數量曲率為s,那麼分量為

式中

所確定的張量場稱為(M,g)的共形曲率張量。
共形曲率張量在共形對映下不變,由平坦度量gij=δij決定的共形曲率張量恆為零,所以共形平坦黎曼流形的共形曲率張量等於零。實際上,有下面的更進一步的結論:n(n>3)維的黎曼流形是共形平坦的充要條件為它的共形曲率張量等於零。常曲率空間總是共形平坦的。
設ƒ是n維黎曼流形(M,g)到m維黎曼流形(N,g┡)的с2階對映。在區域性座標系{U,x}嶅M和{V,y}嶅N下,ƒ可以表示為


和

分別表示(M,g)和(N,g┡)的第二類克里斯托費爾符號,那麼用分量

決定的向量場稱為對映ƒ的張力場,當τα呏0(α =1,2,…,m),就稱ƒ為黎曼流形(M,g)到(N, g┡)的調和對映。
調和對映是一類十分重要的對映,有著深刻的幾何意義並和規範場理論有著廣泛的聯絡。例如,當M的維數n=1時,調和對映就是N上的測地線,特別當M=s1時,就是閉測地線;當N 是實數軸時,調和對映就是黎曼流形M上的調和函式;當ƒ是等距浸入或等距嵌入時,調和對映就是極小子流形。
由於τα呏0是一個二階偏微分方程組,因此,調和對映和二階橢圓型偏微分方程的理論有密切的聯絡。
調和對映的存在性基本問題可敘述如下:設ƒ0∶(M,g)→(N,g┡)是黎曼流形間的對映,那麼在ƒ0的同倫類中是否存在調和對映ƒ?
假定M和N 都是緊無邊界流形,J.伊爾斯和J.H.桑普森證明了:當N 具有非正截面曲率時,答案是肯定的,而L.勒梅韋、J.薩克斯和K.K.烏倫貝克證明了:當M的維數等於2,且π21(N)=0時,答案也是肯定的。
如果M和N 都是緊的,而且M有邊界時,R.S.哈密頓首先證明:當N具非正截面曲率時,具有給定邊界值的調和對映是存在的。
也可類似地定義洛倫茨流形和黎曼流形間的調和對映,這在理論物理中有作用,但還很少研究。谷超豪證明了從閔科夫斯基平面到任意完備黎曼流形的調和對映的初始值問題和邊值問題整體解總是存在的。
參考書目
L.P.Eisenhart,RieMannian Geometry,Princeton Univ.Press,Princeton,1949.
S.Kobayashi and K.Nomizu,Foundations of Diff-erential Geometry,Vol,1~2,John Wiley & Sons,New York,1963、1969.
W.Klingenberg,RieMannian Geometry,Walter.de Gruyter,Berlin,1982.
N.J.Hicks, Notes on Differential Geometry,van Vostrand,Princeton,1965.